2月11日12时，《张朝阳的物理课》第二十七期准时开播。搜狐创始人、董事局主席兼CEO张朝阳坐镇搜狐视频直播间，探究双原子分子气体。张朝阳先带着网友复习氢原子薛定谔方程，根据求解得到的能级公式，讨论氢原子的光谱。接着研究两个氢原子组成的氢分子，其电子组成共价键将原子核束缚起来，将此势能在平衡位置展开得到等效的谐振子势，求解对应的薛定谔方程，解得包含振动与转动自由度的能级，通过此分立的能级与选择定则分析氢分子的光谱。

“我们学了那么多理论，解了那么多方程，现在需要应用一下。”张朝阳开门见山，“我们跟氢原子作战了很长时间，今天要讲氢分子，解决双原子分子气体问题。”

氢原子光谱与里德伯常量

他先带着网友，复习氢原子的薛定谔方程，求解得到氢原子的分立能级公式。

他说，“有了能级公式，就可以研究氢原子在各能级之间跃迁所产生的光谱。”通过推导，网友们发现，从初态能级到末态能级跃迁时，发射出的光线的波数为:

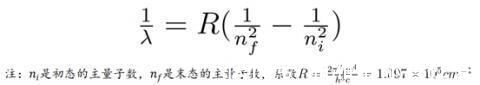
张朝阳解释说，“系数R称为里德伯常量，是量子力学出现之前，人们根据实验测得的氢原子光谱，抽象出的经验公式里得到的，这与用薛定谔方程计算的数值一致。”

他进一步解释，当末态主量子数为1时，末态就是基态，从各激发态到基态的跃迁形成的光谱就是莱曼系，它处于紫外光谱区。当末态主量子数为2时，更高激发态到末态的跃迁形成的光谱是巴尔末系，此线系处于可见光谱区，所以首先被发现。以此类推，可以得到其它谱系。

解薛定谔方程得到氢原子能级，导出的光谱与实验相符，重现了量子力学出现之前的各种线系，他说，“这证明了薛定谔方程的正确性。”

求解氢分子原子核的薛定谔方程

讨论完氢原子的光谱，再来讨论由氢原子组成的氢分子的情况。

“氢分子体系比氢原子复杂多了，它包含了两个氢原子核与两个电子，这四个粒子之间两两都有库伦势相互作用，直接解对应的薛定谔方程非常复杂。”张朝阳指出推导的难度所在和解决方案，“不过，由于电子质量远远小于原子核的质量，分子中电子速度远远大于原子核速度，所以当研究氢分子的振动和转动时，可以把电子看成一种分布，原子核沉浸在这种云一样的分布之中，电子云使得原子核之间具有某种有效的相互作用，从而将原子核结合在一起，这就是所谓的共价键。两个电子是两个原子所共有的。”

经推导发现，这种相互作用与原子核之间的库仑力一起，组成总的有效势能，若振幅较小，可将总有效势能在平衡位置附近做近似展开，得到谐振子势能，那么，重复之前得到的氢原子与谐振子的径向薛定谔方程的步骤，则可得出对应的氢分子中两原子核的径向薛定谔方程:

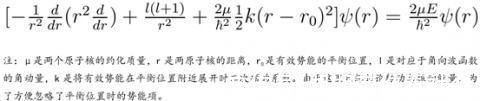
(求解氢分子原子核径向薛定谔方程)

此时，张朝阳先根据解氢原子与谐振子径向薛定谔方程的经验，定义新的函数u为:

再代入到薛定谔方程之中，并将其化简为:

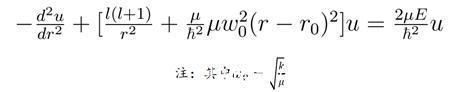
“这个方程有些难解。”张朝阳解释，由于原子核的振动距离非常小，并且转动能远远小于振动能，于是可以近似地将角动量项中的r直接换成平衡距离，若定义新的参数为:

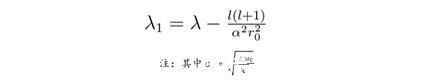
最终，薛定谔方程可以变形为:

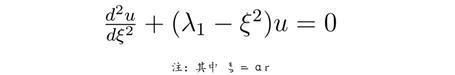
而这正是上节课解一维谐振子薛定谔方程时遇到过的微分方程。利用上节课的结论，马上能得到:

其对应的氢分子原子核的振动与转动能级就可以顺势求出:

(推导氢分子的振动转动能级)

氢分子的振动转动光谱:疏中有密，带状分布

“就像氢原子一样，一旦求出了氢分子原子核的振动与转动能级，就可以得出其对应的光谱。”张朝阳引导网友思考，“这里需要引入能级跃迁的选择定则。”也就是说，原子核跃迁前后的主量子数变化为±1，角量子数的变化也为±1。为了方便讨论，张朝阳还引入记号B，将氢分子原子核的振动与转动能级写为: